문제 설명
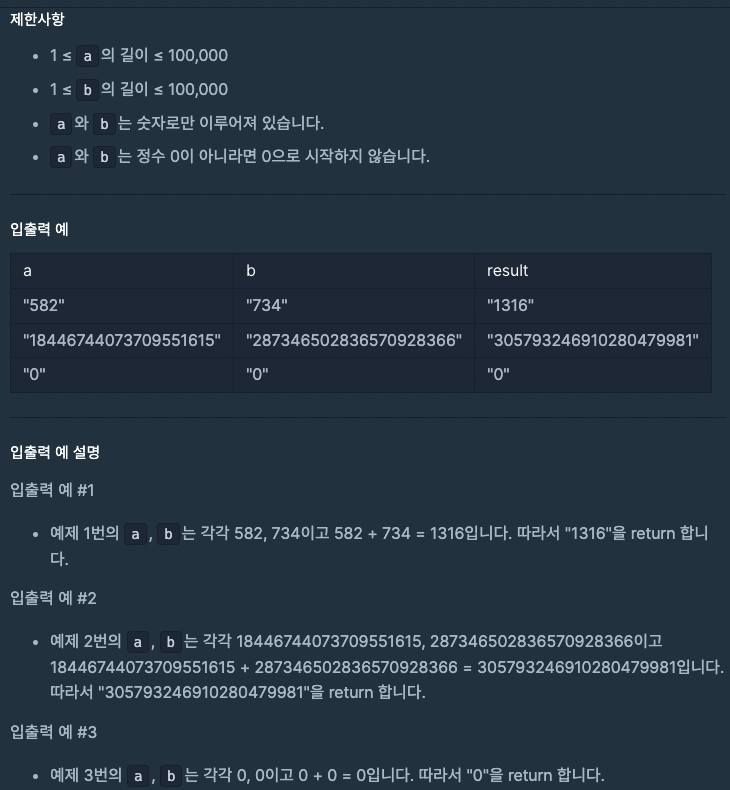
0 이상의 두 정수가 문자열 a, b로 주어질 때, a + b의 값을 문자열로 return 하는 solution 함수를 작성해 주세요.
✅ 내 코드
function solution(a,b){
let toNum = BigInt(a) + BigInt(b);
return toNum.toString()
}
🙋♀️ 내 생각
처음에는 위와 같이 BigInt를 사용해서 풀 생각을 못하고 바로 Number로 바꿔서 풀었다.
코드는 아래와 같다.
function solution(a, b) {
let toNum = Number(a) + Number(b)
return toNum.toString()
}
위와 같이 단순히 Number로 바꾸는 메서드를 사용하면, 숫자가 짧을 경우에는 문제가 없지만,
숫자의 길이가 길어지면 아래와 같이 값이 달라지는 문제가 발생한다. (테스트2와 같은 문제)

전에 이러한 문제가 있다는 것을 얼핏 들은적은 있었지만 깊게 공부한 적은 없어서 몰랐는데 이번 기회에 깊게 공부해보았다.
평소에 들어서 알고 있었던 것은 아래와 같이 숫자의 합의 결과가 true가 나와야하는 상황에서도 false가 나온다는 것이다.
정확히 어떤 경우에 이런 문제가 발생하는지 그리고 왜 발생하는지는 몰랐는데 이 문제를 해결하면서 알게되었다.

💻 학습한것
🔍 원인: 2진법으로 저장되는 특성 / 부동소수점
컴퓨터는 0과 1밖에 모르기때문에 우리가 10진수로 값을 넣어도 결국 컴퓨터는 2진수로 저장한다.
자바스크립트는 숫자를 저장할때, 2진수로 바뀌는 과정에서 부동소수점 형식을 사용한다.
부동소수점 형식은 정수와 소수부분을 나누어 저장하는 방식으로 유리수를 근사적으로 표현할 수 있다.
부동소수점이란 떠돌이 소수점이라고도 부르는데, 말그대로 소수점의 위치를 고정하지 않고 위치를 나타내는 방식을 말한다.
형식은 부호부, 지수부, 가수부 이렇게 구성되어있다.

이런식으로만 보면 이해가 어려우므로 예시를 들어보면,
수: −118.625 (십진법)의 수를 컴퓨터에 저장하면,
이 값은 -1110110.101의 2진법으로 변환되어 저장된다.
부호부: 1 (음수)
부호부에는 음수인지, 양수인지가 저장된다.
-1110110.101 은 부동소수점 방식으로 저장되는데, 1.110110101×2⁶ 이다.
소수점을 왼쪽으로 이동시켜 왼쪽에는 1만 남게된다.
지수부
위의 값을 보면 2의 6승 ➡️ 2의 지수가 6인것을 확인할 수 있다. 이 6이 바로 지수부에 들어가는데 이것도 그냥 들어가는 것이 아니라 변환이 되어들어간다. 32비트 IEEE 754 형식에서는 Bias는 127이므로 6+127 = 133이 된다. 이진법으로 변환하면 10000101이 된다.
(JavaScript에서는 64비트 부동소수점 형식인 IEEE 754 표준을 사용)
가수부
가수부는 소수점의 오른쪽 부분으로, 부족한 비트 수 부분만큼 0으로 채워 23비트로 만든다.
결과는 11011010100000000000000이 된다.

이러한 과정을 정규화라고 부른다.
이렇게 컴퓨터는 2진법으로 숫자를 변환하고 부동소수점을 이용한다는 특징이 있기때문에 정확한 값이 아니라 유사한 값으로 저장이 된다.
평소에는 크게 문제가 되지는 않지만, 실제로 회사의 코드가 됐을때 실무에서 작은 오차로도 큰 손실을 발생시킬 수 있기때문에 이러한 과정이 있다는 것을 이해하고 어떻게 해결할 수 있는지 알아두면 좋을 것 같다.
해결하는 방법은 여러가지가 있지만 가장 간단한 방법은 라이브러리를 이용하는 것이다.
아니면 메서드를 이용할수도 있다. 나는 프로그래머스에서 문제를 푸는것이기때문에 적절한 메서드를 찾아서 풀었다.
💻 내가 사용한 메서드
BigInt(): Number 원시 값이 안정적으로 나타낼 수 있는 최대치인 2^53 - 1보다 큰 정수를 표현할 수 있는 내장 객체
타입은 bignit (number가 아니다!!)
JavaScript의 Number타입은 64비트의 부동소수점 형식으로 제한된 범위의 숫자를 표현할 수 있다. 이에 따라 정수의 표현범위도 제한되며, 가장 큰 정수는 2^53 -1 까지 표현할 수 있다. 이 범위를 초과하는 큰정수를 Number로 표현하려고 하면 정확성이 손실될 수 있다.
BigInt는 이러한 제한을 극복하기 위해 도입된 기능이다. Number가 표현할 수 있는 범위를 초과하는 정수를 안정적으로 표현할 수 있다.
정수 리터럴의 뒤에 n을 붙이거나(10n) 함수 BigInt()를 호출해 생성
const bigIntNumber = BigInt(9007199254740991);
const bigIntLiteral = 123456789012345678901234567890n;
💻 다른사람 코드중에 배울 것
function solution(a, b) {
var answer = '';
const length = Math.max(a.length, b.length);
a = "0".repeat(length - a.length) + a;
b = "0".repeat(length - b.length) + b;
let add = false;
for(let i = length - 1; i >= 0; i--) {
let num = parseInt(a[i]) + parseInt(b[i]) + (add ? 1 : 0);
add = num >= 10;
if(add) num -= 10;
answer = num + answer;
}
if(add) answer = "1" + answer;
return answer;
}BigInt() 메서드를 이용하면 쉽게 풀수있지만 저런 부동소수점의 특성을 이용해서 메서드를 사용하지 않고 푼 방식이 흥미로워서 공부하였다. 애초에 이 코드를 짠 사람은 2진수로 저장되는 특징 그리고 왜 오차가 발생하는지, 부동소수점이 뭔지를 알고 있었기 때문에 이런 풀이가 가능하였을 것이다.
1. 더 긴 문자열의 길이를 구하고 더 짧은 문자열의 앞에 0을 추가하여 길이를 맞춰준다.
const length = Math.max(a.length, b.length);
문자열의 길이를 계산하기 위해서 a와 b의 문자열의 길이중 더 긴 값을 구했다.
더 긴값을 구하는 이유는 덧셈연산을 수행할때 자리수가 맞지 않은 경우를 위해서이다.
간단한 값으로 예를 들어서 설명하면 이해하기가 편한데, 123 + 4567 과 같은 연산을 한다고하면 이 값을 0123+4567과 같이 맞춰주어야 정확하게 계산이 되기 때문이다.
a = "0".repeat(length - a.length) + a;
b = "0".repeat(length - b.length) + b;repeat()을 사용해서 (더긴길이 - a/b의 길이)의 수만큼 0을 만들어서 자릿수를 맞춘다.
a든 b든 길이값이 이미 Max이면 0이 repeat되지 않고, 차이만큼 0이 repeat될 것이다.
2. for문을 돌면서 맨뒷부분부터 더해준다.
초기값을 length-1로 설정하고 i>=0을 해줌으로써 자리수가 맨뒤부터 0까지 반복되도록 했다.
그런데 이때, parseInt()를 사용하여 덧셈을 진행하였는데 이것은 JavaScript의 특성때문이다.
let num = parseInt(a[i]) + parseInt(b[i]) + (add ? 1 : 0);JavaScript에서는 문자열을 더할 때 문자열 연결(concatenation)이 기본 동작이기 때문이다.숫자와 문자열을 더할 때 숫자를 자동으로 문자열로 변환하여 연결한다. 예를 들어, 1 + "2"를 수행하면 결과는 문자열 "12"가 된다.
그래서 parseInt()를 통해 이렇게 문자열을 숫자로 바꾸면서 덧셈을 진행한다. 그리고 만약 더한값이 10이 넘어간다면, add라는 변수를 실행시켜 다음자리수로의 올림을 해준다.
3. 올림값을 변수에 저장해서 carry(올림)하기
이 코드에서는 add를 통해서 자리를 올림해서 더하는 방법을 썼는데 이부분을 이해하는데 시간이 오래 걸렸다.
그래서 비슷하게 변수에는 저장하지만 약간은 다른 방법으로 올림을 만드는 방식을 새로 만들어서 공부했다.
돌아가는 방식이나 거의 유사하지만 올림값과 현재자리수를 계산하는 방식만 바꾸었다.
function solution(a, b) {
let answer = '';
let carry = 0; // 올림값을 저장할 변수
const length = Math.max(a.length, b.length);
a = "0".repeat(length - a.length) + a;
b = "0".repeat(length - b.length) + b;
for (let i = length - 1; i >= 0; i--) {
let num = parseInt(a[i]) + parseInt(b[i]) + carry;
carry = Math.floor(num / 10); // 올림값 계산
num %= 10; // 현재 자리수의 숫자 계산
answer = num + answer;
}
if (carry) {
answer = carry + answer;
}
return answer;
}올림을 해줄 변수를 carry라는 이름을 지어주고 일단 초기값으로 0을 넣는다.
그 다음에는 위의 코드와 같게 짜서 각각의 값을 더해주는데 carry를 통해서 올림값을 전달한다.
초기상태에는 carry가 무조건 0이기때문에 0이 들어갈 것이다.
이해를 쉽게 하기위해, 999와 888을 더한다고 예시를 들어서 보겠다.
- 초기 상태:
- a: "999"
- b: "888"
- answer: ""
- carry: 0
- 문자열을 같은 길이로 맞춘다:
- a: "0999"
- b: "0888"
- 반복문을 통해 자릿수별로 덧셈을 수행:
- 1의 자리 수: 9 + 8 + 0 (carry) = 17
- 현재 자리수의 숫자: 17 % 10 = 7
- 올림값: Math.floor(17 / 10) = 1
- answer: "7"
- carry: 1
- 10의 자리 수: 9 + 8 + 1 (carry) = 18
- 현재 자리수의 숫자: 18 % 10 = 8
- 올림값: Math.floor(18 / 10) = 1
- answer: "87"
- carry: 1
- 100의 자리 수: 9 + 8 + 1 (carry) = 18
- 현재 자리수의 숫자: 18 % 10 = 8
- 올림값: Math.floor(18 / 10) = 1
- answer: "887"
- carry: 1
- 1000의 자리 수: 0 + 0 + 1 (carry) = 1
- 현재 자리수의 숫자: 1 % 10 = 1
- 올림값: Math.floor(1 / 10) = 0
- answer: "1887"
- carry: 0
- 1의 자리 수: 9 + 8 + 0 (carry) = 17
- 올림값이 남아있는 경우, 최종 결과에 추가:
- carry 값이 0이므로 추가 작업 없음.
- 최종 결과:
- answer: "1887"
이런식으로 코드가 돌아가면서 각자리의 수를 더하고 올림값을 계산한다.
🙋♀️ 내 생각
메서드를 이용하면 쉽게 코드를 짤 수 있지만 다른 방법도 공부해보았다.
아직 배우고 있는 과정이기때문에 항상 이런식으로 깊게 공부할 수 만은 없겠지만, 개발자는 꾸준히 공부를 하여야하고 언젠가는 알아야할 내용이라고 생각한다. 단순히 코드를 짜는 것 뿐만아니라 컴퓨터에 대한 이해, 언어에 대한 이해도 함께해야 더 좋은 코드를 짤 수 있는 개발자가 될것이라 생각하고 미래에 그런 개발자가 되고 싶다.
'JavaScript > 알고리즘' 카테고리의 다른 글
| 프로그래머스 이어붙인수 JS ( filter(), reduce(), String(), Number() ) (0) | 2023.06.04 |
|---|---|
| 프로그래머스 주사위 게임 1 JS ( if문, Math.ab() ) (0) | 2023.06.04 |
| 프로그래머스 배열만들기1 JS ( Math.floor(), for문, push() ) (0) | 2023.05.31 |
| 프로그래머스 원소들의 곱과 합 JS ( reduce(), if문 ) (0) | 2023.05.31 |
| 프로그래머스 수 조작하기1 JS ( for문, if문 / reduce() ) (1) | 2023.05.31 |